This article is part of series Let’s make an A3C.
Introduction
In the previous article we built necessary knowledge about Policy Gradient Methods and A3C algorithm. This time we implement a simple agent with our familiar tools - Python, Keras and OpenAI Gym. However, more low level implementation is needed and that’s where TensorFlow comes to play.
The environment is the same as in DQN implementation - CartPole. Final code fits inside 300 lines and is easily converted to any other problem. A3C algorithm is very effective and learning takes only 30 seconds on a regular notebook.
The code presented here however isn’t the original vanilla A3C algorithm, but it has multiple advances incorporated into it. Notably, it leverages the use of GPU with a custom implementation inspired by recent NVIDIA work1 and n-step return.
The complete code is available at GitHub.
N-step return
Before we delve into the implementation itself, let’s explain one more concept.
Usually we used something called 1-step return when we computed Q(s, a), V(s) or A(s, a) functions. That means that we looked only one step ahead. For example, when setting a target of a value function:
\[V(s_0) \xrightarrow{} r_0 + \gamma V(s_1)\]In this case we used an immediate return from \((s_0, a_0, r_0, s_1)\) sample and an estimated value of the function in the next step to give us an approximation. However, we can use more steps to give us another approximation:
\[V(s_0) \xrightarrow{} r_0 + \gamma r_1 + \gamma^2 V(s_2)\]or in general a n-step return:
\[V(s_0) \xrightarrow{} r_0 + \gamma r_1 + ... + \gamma^n V(s_n)\]The n-step return has an advantage that changes in the approximated function get propagated much more quickly. Let’s say that the agent experienced a transition with unexpected reward. In 1-step return scenario, the value function would only change slowly one step backwards with each iteration. In n-step return however, the change is propagated n steps backwards each iteration, thus much quicker.
N-step return has its drawbacks. It’s higher variance because the value depends on a chain of actions which can lead into many different states. This might endanger the convergence.
We can also compute it only when enough samples are available, thus it is delayed. As we know, A3C algorithm needs its samples to be made by current policy and by the time we can compute n-step return the policy might have slightly changed. So this delay introduces some deviation and also threatens the convergence.
We need to keep these properties in mind when introducing n-step return. In practice, however, reasonable values of n help.
Implementation
Let’s first see the big picture. The A3C algorithm contains several key concepts that all make it work. Multiple separate environments are run in parallel, each of which contains an agent. The agents however share one neural network. Samples produced by agents are gathered in a queue, from where they are asynchronously used by a separate optimizer thread to improve the policy. The diagram below shows how these components work together:

We will implement four classes - Environment, Agent, Brain and Optimizer. Two of these are thread classes - Environment and Optimizer.
Environment :Thread
run() # runs episodes in loop
Agent
act(s) # decides what action to take in state s
train(sample) # processes sample and add it to the train queue
Brain
predict(s) # outputs pi(s) and V(s)
train_push(sample) # adds sample to the training queue
optimize() # does the gradient descent step
Optimizer :Thread
run() # calls brain.optimize() in loop
Environment
The Environment class is an instance of OpenAI Gym environment and contains an instance of Agent. It is also a thread that continuously runs one episode after another.
def run(self):
while not self.stop_signal:
self.runEpisode()
The runEpisode() method is simple:
def runEpisode(self):
s = self.env.reset()
while True:
time.sleep(THREAD_DELAY) # yield
a = self.agent.act(s)
s_, r, done, info = self.env.step(a)
if done: # terminal state
s_ = None
self.agent.train(s, a, r, s_)
s = s_
if done or self.stop_signal:
break
The THREAD_DELAY parameter controls a delay between steps and enables to have more parallel environments than there are CPUs. High number of agents is crucial for convergence of the algorithm as the gradient approximation quality depends on high diversity of samples.
Agent
In Agent class, the act() method returns an action to take. To support exploration, it implements ε-greedy policy with linearly decreasing rate. The action is selected according to the policy distribution returned by the neural network.
def act(self, s):
if random.random() < epsilon:
return random.randint(0, NUM_ACTIONS-1)
else:
p = brain.predict_p(s)
return np.random.choice(NUM_ACTIONS, p=p)
The train() method receives samples, processes them and pushes them into the training queue. First, it turns actions into one hot encoded array needed later. Then it stores the current transition in an internal memory, which is used to compute the n-step return.
def train(self, s, a, r, s_):
a_cats = np.zeros(NUM_ACTIONS)
a_cats[a] = 1
self.memory.append( (s, a_cats, r, s_) )
Last n samples are stored in this buffer and when there are enough of them, n-step discounted reward R is computed. Proper variables are retrieved and a tuple \((s_0, a_0, R, s_n)\) is inserted into the brain’s training queue.
if len(self.memory) >= N_STEP_RETURN:
s, a, r, s_ = get_sample(self.memory, N_STEP_RETURN)
brain.train_push(s, a, r, s_)
self.memory.pop(0)
An internal get_sample() function is responsible to compute n-step discounted reward and return a proper tuple:
def get_sample(memory, n):
r = 0.
for i in range(n):
r += memory[i][2] * (GAMMA ** i)
s, a, _, _ = memory[0]
_, _, _, s_ = memory[n-1]
return s, a, r, s_
The last thing we have to deal with is the case when our agent encounters a terminal state. As there will be no more states after, we have to deplete the whole buffer. In loop, we shorten the buffer in each iteration and compute the n-step return, where n is equal to the current length of the buffer.
if s_ is None: # terminal state
while len(self.memory) > 0:
n = len(self.memory)
s, a, r, s_ = get_sample(self.memory, n)
brain.train_push(s, a, r, s_)
self.memory.pop(0)
Effective implementation
You might have noticed that we are looping over the whole memory within each step to compute the discounted reward. While this implementation is good for demonstration and understanding, it is clearly inefficient. Let’s look at the discounted reward formula:
\[R_0 = r_0 + \gamma r_1 + \gamma^2 r_2 + ... + \gamma^{n-1} r_{n-1}\] \[R_1 = r_1 + \gamma r_2 + \gamma^2 r_3 + ... + \gamma^{n-1} r_{n}\]We can see a relationship:
\[R_1 = \frac{R_0 - r_0}{\gamma} + \gamma^{n-1} r_n\]So we can remember the value of R and update it accordingly with each time step. This implementation is used in the actual accompanying code.
Brain
The Brain class encapsulates the neural network, TensorFlow graph definition and related computation. Let’s look at its parts in order.
Training queue
One of the responsibilities of the Brain class is to hold a training queue. This queue consists of 5 arrays - starting state s, one-hot encoded taken action a, discounted n-step return r, landing state after n steps s_ and a terminal mask with values 1. or 0., indicating whether the s_ is None or not. Terminal mask will be useful later to parallelize the computation.
def train_push(self, s, a, r, s_):
with self.lock_queue:
self.train_queue[0].append(s)
self.train_queue[1].append(a)
self.train_queue[2].append(r)
if s_ is None:
self.train_queue[3].append(NONE_STATE)
self.train_queue[4].append(0.)
else:
self.train_queue[3].append(s_)
self.train_queue[4].append(1.)
Also a dummy NONE_STATE is used in case the s_ is None. This dummy state is valid, so it can be processed by the neural network, but we don’t care about the result. It’s only there to parallelize the computation.
The samples from agents are gathered in the training queue through train_push() method in a synchronized manner.
Neural network
The core of our new agent is a neural network that decides what to do in a given situation. There are two sets of outputs - the policy itself and the value function.
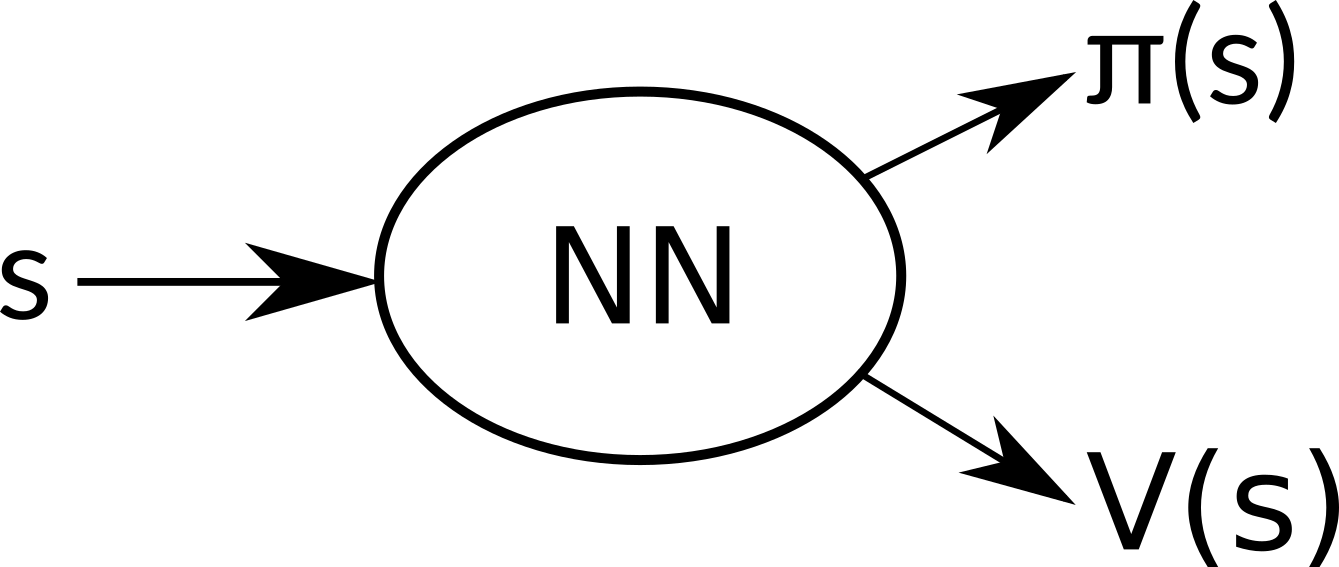
It is defined very easily with Keras:
l_input = Input( batch_shape=(None, NUM_STATE) )
l_dense = Dense(16, activation='relu')(l_input)
out_actions = Dense(NUM_ACTIONS, activation='softmax')(l_dense)
out_value = Dense(1, activation='linear')(l_dense)
model = Model(inputs=[l_input], outputs=[out_actions, out_value])
The policy output goes through softmax activation to make it correct probability distribution. The ouput for value function is linear, as we need all values to be possible.
Loss function
Now we have to define a loss function, which has three parts:
\[L = L_{\pi} + c_v L_v + c_{reg} L_{reg}\]\(L_{\pi}\) is the loss of the policy, \(L_v\) is the value error and \(L_{reg}\) is a regularization term. These parts are multiplied by constants \(c_v\) and \(c_{reg}\), which determine what part we stress more. Let’s describe these in order.
Policy Loss
We defined an objective function \(J(\pi)\) as total reward an agent can achieve under policy \(\pi\) averaged over all starting states:
\[J(\pi) = E_{\rho^{s_0}}[V(s_0)]\]We also know that a gradient of this function is determined by Policy Gradient Theorem as:
\[\nabla_\theta\;J(\pi) = E_{s\sim\rho^\pi,\;a\sim{\pi(s)}}[ A(s, a) \cdot \nabla_\theta\;log\;\pi(a\|s) ]\]We are trying to maximize the J function, so we can just say that:
\[L_\pi = -J(\pi)\]However, TensorFlow can’t analytically compute gradient of this function, so we have to help it with our knowledge. We can rewrite the definition of function J as follows, while treating the \(\underline{A(s, a)}\) part as a constant:
\[J(\pi) = E [\underline{A(s, a)} \cdot log\;\pi(a\|s)]\]This expression can be automatically differentiated by TensorFlow resulting in the same formula as given by the Policy Gradient Theorem.
For completeness, we have to swap the expectation for average over all samples in a batch. We are using samples generated by policy π and therefore can make this switch. The final loss function is then:
\[L_\pi = - \frac{1}{n} \sum_{i=1}^{n} \underline{A(s_i, a_i)} \cdot log\;\pi(a_i|s_i)\]Value loss
Learning the value function V(s) is analogous to Q-learning case, where we tried to learn action-value function Q(s, a). In n-step return scenario, we know that the true function V(s) should meet the Bellman equation:
\[V(s_0) = r_0 + \gamma r_1 + \gamma^2 r_2 + ... + \gamma^{n-1} r_{n-1} + \gamma^n V(s_n)\]The approximated V(s) should converge according to this formula and we can measure the error as:
\[e = r_0 + \gamma r_1 + \gamma^2 r_2 + ... + \gamma^{n-1} r_{n-1} + \gamma^n V(s_n) - V(s_0)\]Then we can define the \(L_V\) as a mean squared error of all given samples as:
\[L_V = \frac{1}{n}\sum_{i=1}^{n} e_i^2\]Regularization with policy entropy
Adding entropy to the loss function was found to improve exploration by limiting the premature convergence to suboptimal policy2. Entropy for policy \(\pi(s)\) is defined as:
\[H(\pi(s)) = - \sum_{k=1}^{n} \pi(s)_k \cdot log\;\pi(s)_k\]Where \(\pi(s)_k\) is a probability for k-th action in state s. It’s useful to know that entropy for fully deterministic policy (e.g. [1, 0, 0, 0] for four actions) is 0 and it is maximized for totally uniform policy (e.g. [0.25, 0.25, 0.25, 0.25]).
Knowing this we see that by trying to maximize the entropy, we are keeping the policy away from the deterministic one. This fact stimulate exploration.
Averaging over all samples in a batch, \(L_{reg}\) is then set to:
\[L_{reg} = - \frac{1}{n}\sum_{i=1}^{n} H(\pi(s_i))\]TensorFlow graph
So, how do we actually implement all of the above? We need to define a TensorFlow graph of the loss function that allows it’s analytical computation.
First we need placeholders, that will be filled with relevant data when a minimize operation is run. They represent a 2D array and will hold a whole batch. The first dimension represent different samples in a batch and is unlimited. The second dimension is different for each placeholder, representing a dimension of state, one-hot encoded action and reward.
# starting states
s_t = tf.placeholder(tf.float32, shape=(None, NUM_STATE))
# one hot encoded actions
a_t = tf.placeholder(tf.float32, shape=(None, NUM_ACTIONS))
# n-step discounted total reward
r_t = tf.placeholder(tf.float32, shape=(None, 1))
Then we propagate the states through our network to get policy and value outputs. Note that we are actually not running any operation at this time, but rather defining a graph that will be run during the minimize operation.
p, v = model(s_t)
Now let’s recall how does the \(L_\pi\) part of our loss function look like:
\[L_\pi = - \frac{1}{n} \sum_{i=1}^{n} \underline{A(s_i, a_i)} \cdot log\;\pi(a_i|s_i)\]The expression \(log\;\pi(a\|s)\) means a probability of taking action a in state s, or in other words, the a-th index of π(s). Unfortunately, we can’t use indexes when defining TensorFlow graph, but we can use other arithmetic operations. If we take the whole policy, multiply it with one-hot encoded action and sum these together, we get exactly what we need.
logp = tf.log(tf.reduce_sum(p*a_t, axis=1, keep_dims=True) + 1e-10)
We add a small constant to prevent a NaN error that could occur if we selected an action while it’s probability was zero. That could happen, because we are using ε-greedy policy.
We also need to be careful to do desired operations along correct dimensions, yielding desired outputs. TensorFlow is very silent about formal errors and an incorrect reduce operation can happen very easily. Always debug your code when you play with graph implementation and make sure to print out tensor dimensions for each operation.
The other half of the equation is the advantage function. We use a fact that the r_t placeholder holds a value of:
Recall that the n-step advantage function is defined as:
\[A(s, a) = Q(s, a) - V(s)\]We can approximate the Q(s, a) function with samples we observed during an episode, resulting in:
\[A(s, a) = r_0 + \gamma r_1 + \gamma^2 r_2 + ... + \gamma^{n-1} r_{n-1} + \gamma^n V(s_n) - V(s)\]Defining the advantage function is therefore as simple as:
advantage = r_t - v
And finally, we can define the \(L_\pi\) itself. We need to take care to treat the advantage function as constant, by using tf.stop_gradient() operator. Expressions for \(L_\pi\), \(L_V\) and \(L_{reg}\) all include averaging over whole batch. But it can be skipped now and performed as a last step, when we add these together.
loss_policy = - logp * tf.stop_gradient(advantage)
Now we define \(L_V\). Interestingly, the error in this case is the same as the advantage function:
\[e = r_0 + \gamma r_1 + \gamma^2 r_2 + ... + \gamma^{n-1} r_{n-1} + \gamma^n \underline{V(s_n)} - V(s)\]How could that be? It’s because we made the approximation when computing A(s, a). We didn’t compute the expectation over all possible chains, but rather used one sample from a run. Note that \(\underline{V(s_n)}\) has to be a constant to avoid gradient leak (we want to optimize \(V(s)\), not \(V(s_n)\). In our implemenation, it is already a constant, because we filled \(r_t\) through a placeholder. \(L_V\) then become:
loss_value = C_V * tf.square(advantage)
Finally, we have to define the entropy. The formula for \(L_{reg}\) is:
\[L_{reg} = - \frac{1}{n}\sum_{i=1}^{n} H(\pi(s_i))\]Again, we need to take care of the possible NaN error of the log() function, by adding a small constant.
entropy = C_E * tf.reduce_sum(p * tf.log(p + 1e-10), axis=1, keep_dims=True)
Now we add all parts together. In all three formulas above, we skipped the averaging part, but we can compute it now in a single step.
loss_total = tf.reduce_mean(loss_policy + loss_value + entropy)
As a last step, we choose an algorithm that will be used for optimization and define the minimize operation. RMSProp was found to work well and it allows for manual control of learning rate. We have only an approximated gradient in our setting, so we have to proceed in a slow and controlled manner.
optimizer = tf.train.RMSPropOptimizer(LEARNING_RATE, decay=.99)
minimize = optimizer.minimize(loss_total)
Optimizer
Last part of the puzzle is Optimizer. The class itself is very simple, it just a thread that repeatedly calls brain.optimize().
def run(self):
while not self.stop_signal:
brain.optimize()
So, let’s look at this brain.optimize() function. It preprocesses data and run the minimize operation we defined earlier. TensorFlow then computes the gradient and changes neural network’s weights.
First, we have to make sure that we have enough samples in the training queue. This is required to get a good quality approximation of the gradient and it also allows for efficient batch computation. If there aren’t enough samples, we simply yield to other threads to do their work.
def optimize(self):
if len(self.train_queue[0]) < MIN_BATCH:
time.sleep(0) # yield
return
Then we extract all the samples from the queue in a synchronized manner:
with self.lock_queue:
s, a, r, s_, s_mask = self.train_queue
self.train_queue = [ [], [], [], [], [] ]
And process them into solid blocks of numpy arrays:
s = np.vstack(s)
a = np.vstack(a)
r = np.vstack(r)
s_ = np.vstack(s_)
s_mask = np.vstack(s_mask)
The reward received from the training queue is only immediate, excluding the \(\gamma^n V(s_n)\) part, so we have to add it.
\[r = r_0 + \gamma r_1 + \gamma^2 r_2 + ... + \gamma^{n-1} r_{n-1}\]Fortunately, this can be efficiently done on GPU for all states in a batch in parallel.
v = self.predict_v(s_)
r = r + GAMMA_N * v * s_mask
First we compute the \(V(s_n)\) for all landing states. Then we add it to the r matrix, again by using vectorized operation.
But, if the landing state is terminal, we shouldn’t add the \(\gamma^n V(s_n)\) term. However, we cleverly prepared the s_mask array that is 0 in case of terminal state and 1 otherwise. This simple trick allows us to still use vectorized operation. Although run on CPU, modern instructions allow for matrix multiplication that is much quicker than a loop implementation. There is only a small overhead by computing the values for NONE_STATE. However, these states are sparse and the cost is small compared to selective computation.
Finally, we extract the placeholders, run the minimize operation and TensorFlow will do the rest.
s_t, a_t, r_t, minimize = self.graph
self.session.run(minimize, feed_dict={s_t: s, a_t: a, r_t: r_})
So, the optimizer runs the minimize operation tirelessly in a loop. However, one optimizer is often not enough. But nothing stops us from running multiple optimizers at the same time. And indeed, in practice two optimizers are much more efficient than one. While one is occupied by running a GPU operation, the other can preprocess the data. One optimizer often struggles to keep pace with incoming data. If it can’t consume incoming samples quickly, the queue keeps growing and it leads to problems.
Main
The main program starts with determining the shape of states and actions in a given environment. This allows for fast switching of environments simply by changing a single constant (at least for simple environments).
env_test = Environment(render=True, eps_start=0., eps_end=0.)
NUM_STATE = env_test.env.observation_space.shape[0]
NUM_ACTIONS = env_test.env.action_space.n
Then it creates instances of Brain, Environment and Optimizer.
brain = Brain()
envs = [Environment() for i in range(THREADS)]
opts = [Optimizer() for i in range(OPTIMIZERS)]
Finally, it just starts the threads, wait given number of seconds, stops them and displays a trained agent to the user.
for o in opts:
o.start()
for e in envs:
e.start()
time.sleep(RUN_TIME)
for e in envs:
e.stop()
for e in envs:
e.join()
for o in opts:
o.stop()
for o in opts:
o.join()
env_test.run()
Remarks
Positive results were experienced when using different exploration constants for different agents2. In this implementation, however, a single value for all agents is used for simplicity.
The results are highly variable. In case of CartPole environment, almost all runs result in a capable agent. However, in general the algorithm is very sensitive to starting conditions and in more complex environments it might result in very variable performance. You should average several runs if you want to measure progress.
This is a table of all constants used in the algorithm:
| Parameter | Value | Explanation |
|---|---|---|
| agent threads | 8 | |
| optimizer threads | 2 | |
| thread delay | 0.001 s | |
| γ | 0.99 | |
| εstart | 0.40 | |
| εstop | 0.15 | |
| εsteps | 75 000 | ε will come down to εstop after εsteps |
| n-step | 8 | |
| minimal batch size | 32 | |
| RMSprop learning rate | 0.005 | |
| cv | 0.5 | LV constant |
| creg | 0.01 | Lreg constant |
| training time | 30s |
Results
I trained the agent on my MacBook with integrated NVIDIA GeForce GT 750M 2048MB GPU. The CPU has four physical cores, but I used 8 agents. The number of agents directly affects the performance, because it influences the quality of the gradient. You should tweak the hyperparameters to work best on your setup.
Training takes 30 seconds during which the algorithm goes through roughly 1000 episodes and 65 000 steps, that corresponds to about 2 200 steps per second. Results averaged over 10 runs are shown below:
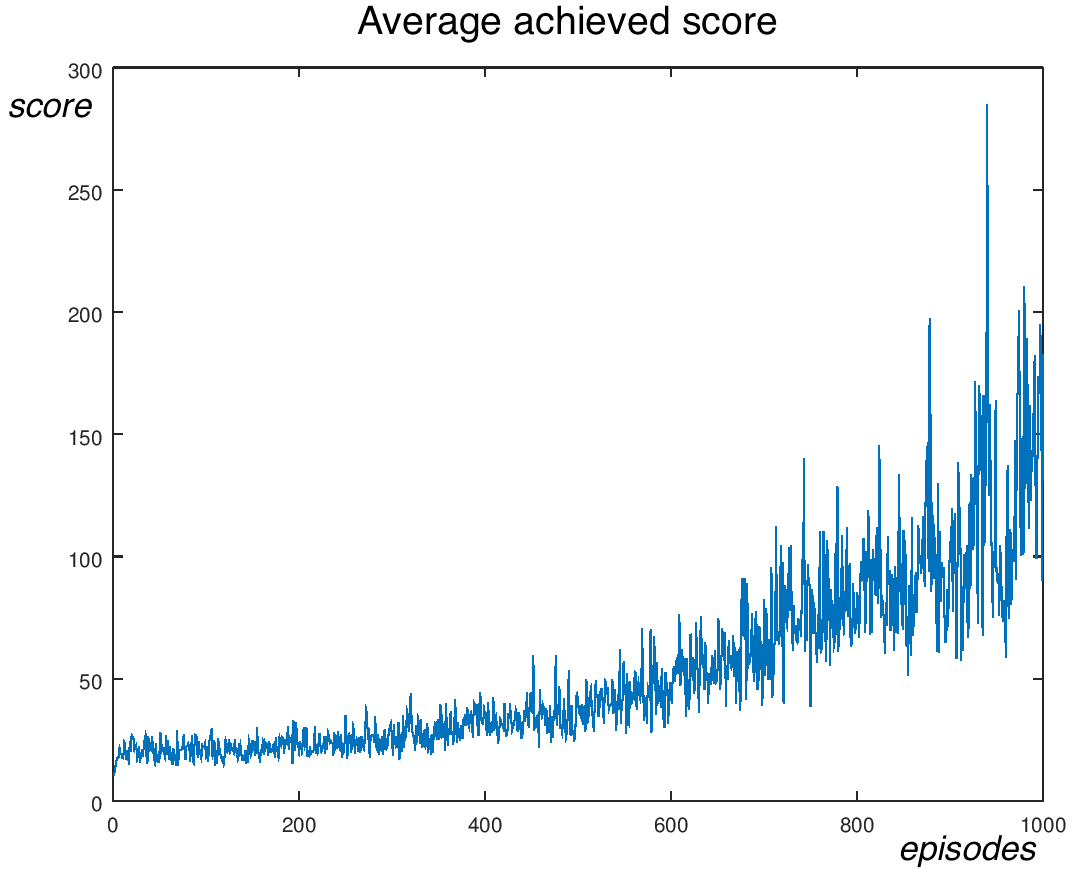
You can see a demonstration how a trained agent behaves below:

You can download the code from GitHub. Feel free to use it as a base for your experiments or developing more capable agents. If you have any other questions, do not hesitate to ask me in comments.