Let’s make a DQN: Theory

Introduction

In February 2015, a group of researches from Google DeepMind published a paper¹ which marks a milestone in machine learning. They presented a novel, so called DQN network, which could achieve breathtaking results by playing a set of Atari games, receiving only a visual input.

In these series of articles, we will progressively develop our knowledge to build a state-of-the-art agent, that will be able to learn to solve variety of tasks just by observing the environment. We will explain the needed theoretical background in less technical terms and then build a program to demonstrate how the theory works in practice.

These articles assume some acquaintance with reinforcement learning and artificial neural networks. For those of you, who are not familiar with these terms, I recommend to have a look at a great book from professor Sutton, 1998² first.

We will use Python to program our agent, Keras library to create an artificial neural network (ANN) and OpenAI Gym toolkit as the environment.

Background

The ultimate goal of reinforcement learning is to find a sequence of actions from some state, that lead to a reward. Undoubtedly, some action sequences are better than others. Some sequences might lead to a greater reward, some might get it faster. To develop this idea more, let’s put it down more formally.

The agent is in a state s and has to choose one action a, upon which it receives a reward r and come to a new state s’. The way the agent chooses actions is called policy.

Let’s define a function Q(s, a) such that for given state s and action a it returns an estimate of a total reward we would achieve starting at this state, taking the action and then following some policy. There certainly exist policies that are optimal, meaning that they always select an action which is the best in the context. Let’s call the Q function for these optimal policies Q*.

If we knew the true Q* function, the solution would be straightforward. We would just apply a greedy policy to it. That means that in each state s, we would just choose an action a that maximizes the function Q* - \(\text{argmax}_a Q^*(s, a)\). Knowing this, our problem reduces to find a good estimate of the Q* function and apply the greedy policy to it.

Let’s write a formula for this function in a symbolic way. It is a sum of rewards we achieve after each action, but we will discount every member with γ:

γ is called a discount factor and when set it to \(\gamma < 1\), it makes sure that the sum in the formula is finite. Value of each member exponentially diminish as they are more and more in the future and become zero in the limit. The γ therefore controls how much the function Q in state s depends on the future and so it can be thought of as how much ahead the agent sees. Typically we set it to a value close, but lesser to one. The actions are chosen according to the greedy policy, maximizing the Q* function. When we look again at the formula, we see that we can write it in a recursive form:

We just derived a so called Bellman equation (it’s actually a variation for action values in deterministic environments).

If we turn the formula into a generic assignment \(Q(s, a) = r + \gamma \max_a Q(s', a)\) we have a key idea of Q-learning introduced by Watkins, 1989³. It was proven to converge to the desired Q*, provided that there are finite number of states and each of the state-action pair is presented repeatedly⁴.

This is great news. It means that we could use this assignment every time our agent experience a new transition and over time, it would converge to the Q* function. This approach is called online learning and we will discuss it in more detail later.

However, in the problems we are trying to solve, the state usually consists of several real numbers and so our state space is infinite. These numbers could represent for example a position and velocity of the agent or, they could mean something as complex as RGB values of a current screen in an emulator.

We can’t obviously use any table to store infinite number of values. Instead, we will approximate the Q function with a neural network. This network will take a state as an input and produce an estimation of the Q function for each action. And if we use several layers, the name comes naturally - Deep Q-network (DQN).

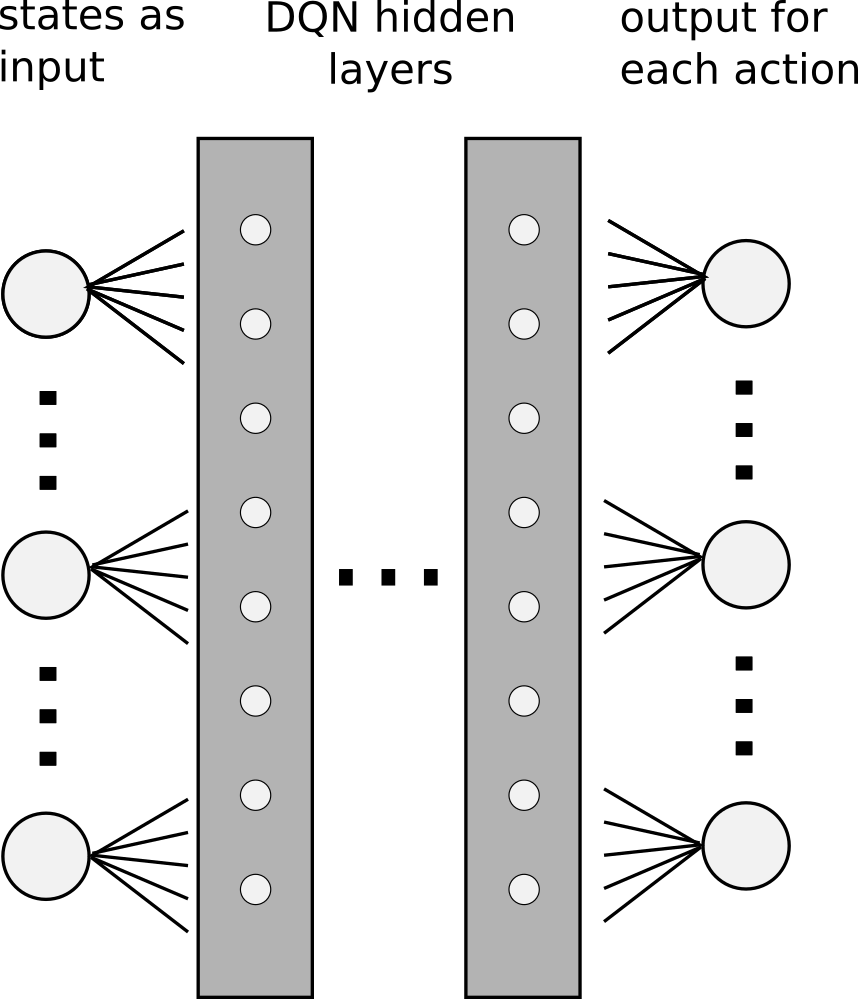
But the original proof about the convergence does not hold anymore. Actually, the authors of the original research acknowledged that using a neural network to represent the Q function is known to be unstable¹. To face with this issue, they introduced several key ideas to stabilize the training, which are mainly responsible for the success we see. Let’s present first of them.

Experience replay

During each simulation step, the agent perform an action a in state s, receives immediate reward r and come to a new state s’. Note that this pattern repeats often and it goes as (s, a, r, s’). The basic idea of online learning is that we use this sample to immediately learn from it.

Because we are using a neural network, we can’t simply use the assignment

but instead, we can shift our estimation towards this target:

We can do it by performing a gradient descend step with this sample. We intuitively see that by repeating this many times, we are introducing more and more truth into the system and could expect the system to converge. Unfortunately, it is often not the case and it will require some more effort.

The problem with online learning is that the samples arrive in order they are experienced and as such are highly correlated. Because of this, our network will most likely overfit and fail to generalize properly.

The second issue with online learning is that we are not using our experience effectively. Actually, we throw away each sample immediately after we use it.

The key idea of experience replay⁵ is that we store these transitions in our memory and during each learning step, sample a random batch and perform a gradient descend on it. This way we solve both issues.

Lastly, because our memory is finite, we can typically store only a limited number of samples. Because of this, after reaching the memory capacity we will simply discard the oldest sample.

Exploration

If we always followed the greedy policy, we might never find out that some actions are better then others. A simple technique to resolve this is called ε-greedy policy. This policy behaves greedily most of the time, but chooses a random action with probability ε. The interesting fact here is that using the previously introduced update formula still shifts the estimated Q function towards the optimal Q* function, even if we use ε-greedy policy to acquire new experience. This is caused by the max in the formula. Because we are not learning the Q function for the policy we are using, but Q* instead, the method is called to be off-policy.

Implementation

Is it enough to get us started? An earlier research⁶ shows us it is. In the next chapter, we will implement a simple Q-network that will solve a famous cart-pole problem.

References